Program Description
B-EYE simulates the optics of a honey bee's (Apis mellifera) eye. It is based on findings of a number of anatomical and behavioural studies*. I will not go into the biological details of how the bee's eye works here. Instead I will quickly go through the steps of my program to show how a bee would see an ant, as an example. The ant is taken from an illustration by MC Escher.
The program's input consists of a grey scale image of the pattern which the [model] bee is looking at and a set of parameters determining the bee's position, the dimensions of the pattern, the desired form of output etc. In our case the image is that shown in fig. 1 , its horizontal edge would be 2cm long, and the bee is positioned at a distance of 2cm directly in front of it.
Figure 1
B-EYE's first step is to project the flat input image onto the hemisphere of the bee's frontal visual field, positioned between the bee and the pattern and centred around the bee. (The bee's visual field is actually much bigger, but the pattern will always be in front of the bee, so we need not look backwards. ) Depending on how close the bee is to the pattern (relative to the pattern's size), this step can distort the pattern quite significantly. In fig. 2 we are viewing the projected image on the hemisphere. The bee is inside, looking out of the screen towards the lower left corner, while we are outside, somewhere close to the pattern.
Figure 2
The next step is where the bee's optics come into play. Bees, like most other insects, have compound eyes, ie. arrays of hundreds of single eyes, each with its own lens and each looking in a different direction. To model this, B-EYE uses a single array of ommatidia (single eyes) in which all of the relevant parameters (angles between ommatidia, visual fields of ommatidia) are the same as in the real bee. This model eye now looks at the projected image on the hemisphere. (The model bee could just as well look at the original picture, but the projection onto a hemisphere reduces the processing time dramatically.) Fig. 3 shows the result of this step, where each single dot depicts the grey level that the respective ommatidium perceives. In the inset the dots were expanded to fill in the gaps.
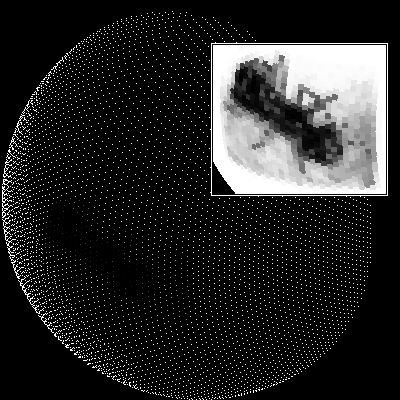Figure 3
The ommatidia of real bees' eyes are arranged in a hexagonal array. But because the ommatidia look in directions which are not necessarily radial with respect to the centre of the bee's head, this array does not correspond to the one in fig. 3. Therefore, if we want to know what a bee sees at the level of the retina, we have to display the array as it is on the eye's surface, which is the last step of B-EYE. Fig. 4 shows the final output, a hexagonal array of patches, each patch corresponding to one ommatidium. The white area represents the hemisphere of the bee's frontal visual field.
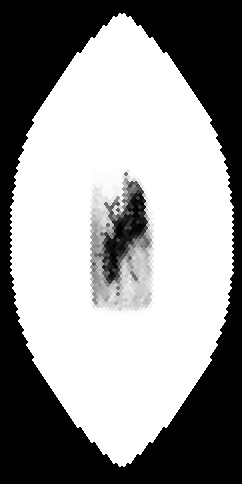Figure 4
Notice that B-EYE treats its input always as a two-dimensional image. The view of a real (ie. three-dimensional) ant would only be slightly different in our example, but this difference can become significant if the bee gets very close to the object.
*
*
* Pages with interactive content are not available in this reconstructed site, sorry.